
Implicit Differntiation Quiz Quizizz
Ex 56, 1 If x and y are connected parametrically by the equations without eliminating the parameter, Find 𝑑𝑦/𝑑𝑥, x = 2〖𝑎𝑡〗^2, y = 〖𝑎𝑡〗^4Here 𝑑𝑦/𝑑𝑥 = (𝑑𝑦/𝑑𝑡)/ (𝑑𝑥/𝑑𝑡) Calculating 𝒅𝒚/𝒅𝒕 𝑦 = 〖𝑎𝑡〗^4 𝑑𝑦/𝑑𝑡 " ="Suppose xy=4 and dy/dt=2 Find dx/dt when x=3 y x (dy/dx) = 0 by implicit differentiation We are given with the expression xy = 4 The first derivative of the x is dx/dt while that of y is dy/dt in this case using the multiplication rule of differentiation and that of constants, x dy/dt y dx/dt = 0 when x= 3, y should be 4/3
(x+y)^2=4 find dy/dx
(x+y)^2=4 find dy/dx- Ex 94, 9 For each of the differential equations in Exercises 1 to 10, find the general solution 𝑑𝑦/𝑑𝑥=sin^(−1)𝑥 𝑑𝑦/𝑑𝑥=sin^(−1)𝑥 𝑑𝑦 = sin^(−1)𝑥 dx Integrating both sides ∫1 〖𝑑𝑦 〗= ∫1 〖sin^(−1)〖𝑥1 𝑑𝑥〗 〗 y = sin−1 x ∫1 〖1 𝑑𝑥 −∫1 1/√(1 − 𝑥^2 ) ∫1 〖1𝑑𝑥 〗 〗 dx IntegratinSolve your math problems using our free math solver with stepbystep solutions Our math solver supports basic math, prealgebra, algebra, trigonometry, calculus and more
Secure Media Collegeboard Org
If y is a function of x then dy dx is the derivative meaning the gradient (slope of the graph) or the rate of change with respect to x 02 Functions of 2 or more variables Functions which have more than one variable arise very commonly Simple examples are † formula for the area of a triangle A = 1 2 bh is a function of the two variables, base b and height h † formula for electrical Explanation This is a first order separable differential equation dy dx = y2 −4 dy y2 −4 = dx ∫ dy y2 − 4 = ∫dx Perform partial fraction 1 y2 −4 = A y 2 B y − 2 = A(y − 2) B(y 2) (y2 − 4) Compare the numeratorsFind dy/dx y^2(y^24)=x^2(x^25) Differentiate both sides of the equation Differentiate the left side of the equation Tap for more steps Differentiate using the Product Rule which states that is where and By the Sum Rule, the derivative of with respect to is Differentiate using the chain rule, which states that is where and Tap for more steps To apply the Chain Rule, set as
Answer (1 of 10) dy/dx=(xy1)^2(1) Let xy1=t 1dy/dx=dt/dx dy/dx=dt/dx 1(2) from eqn(1) & (2) dt/dx1=t^2 dt/dx=1t^2 1dt/(1t^2)=dxOur online expert tutors can answer this problem Get stepbystep solutions from expert tutors as fast as 1530 minutes Your first 5 questions are on us!When applying Formula (3), keep in mind that the only values of x and y that can be substituted into the righthand side of Formula (3) are those values
(x+y)^2=4 find dy/dxのギャラリー
各画像をクリックすると、ダウンロードまたは拡大表示できます
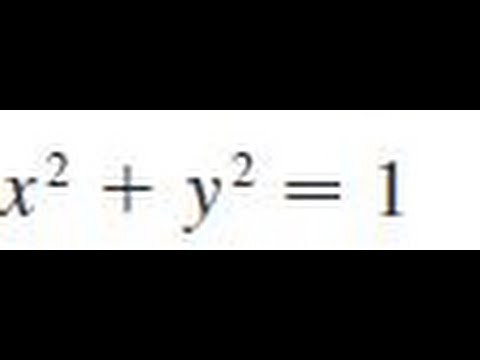 Secure Media Collegeboard Org | 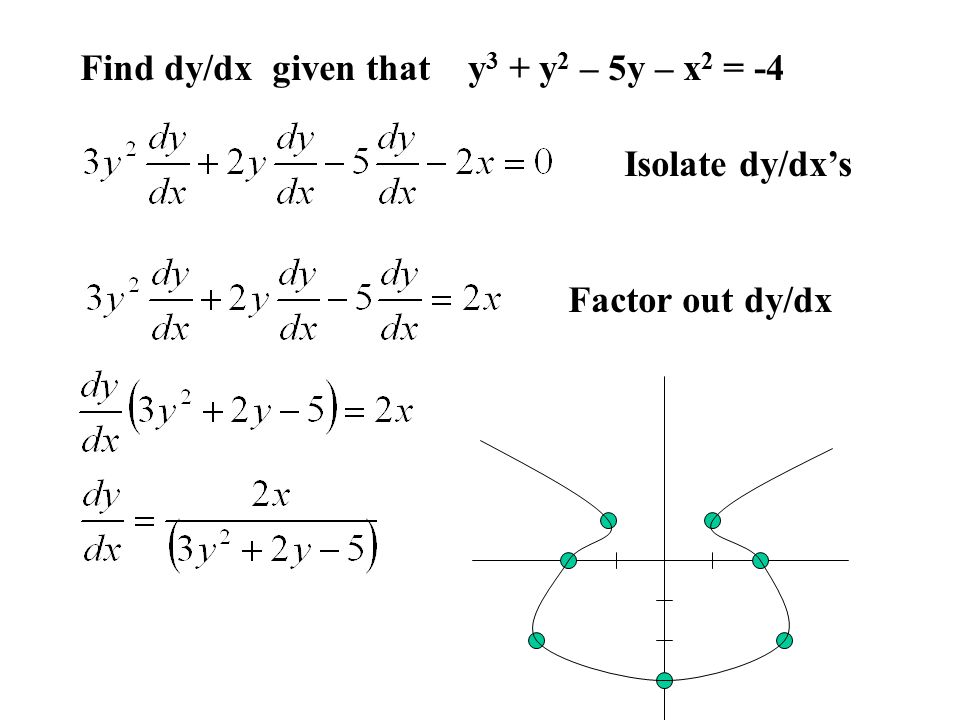 Secure Media Collegeboard Org | Secure Media Collegeboard Org |
Secure Media Collegeboard Org |  Secure Media Collegeboard Org |  Secure Media Collegeboard Org |
 Secure Media Collegeboard Org |  Secure Media Collegeboard Org |  Secure Media Collegeboard Org |
Secure Media Collegeboard Org | Secure Media Collegeboard Org |  Secure Media Collegeboard Org |
 Secure Media Collegeboard Org | Secure Media Collegeboard Org | Secure Media Collegeboard Org |
 Secure Media Collegeboard Org | Secure Media Collegeboard Org |  Secure Media Collegeboard Org |
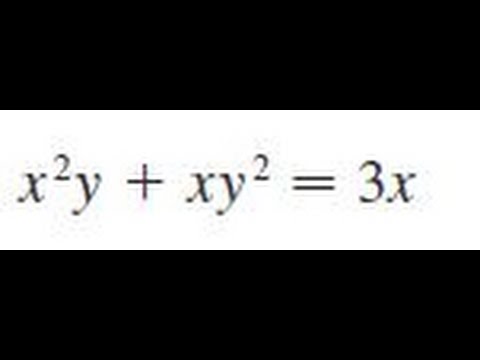 Secure Media Collegeboard Org |  Secure Media Collegeboard Org | 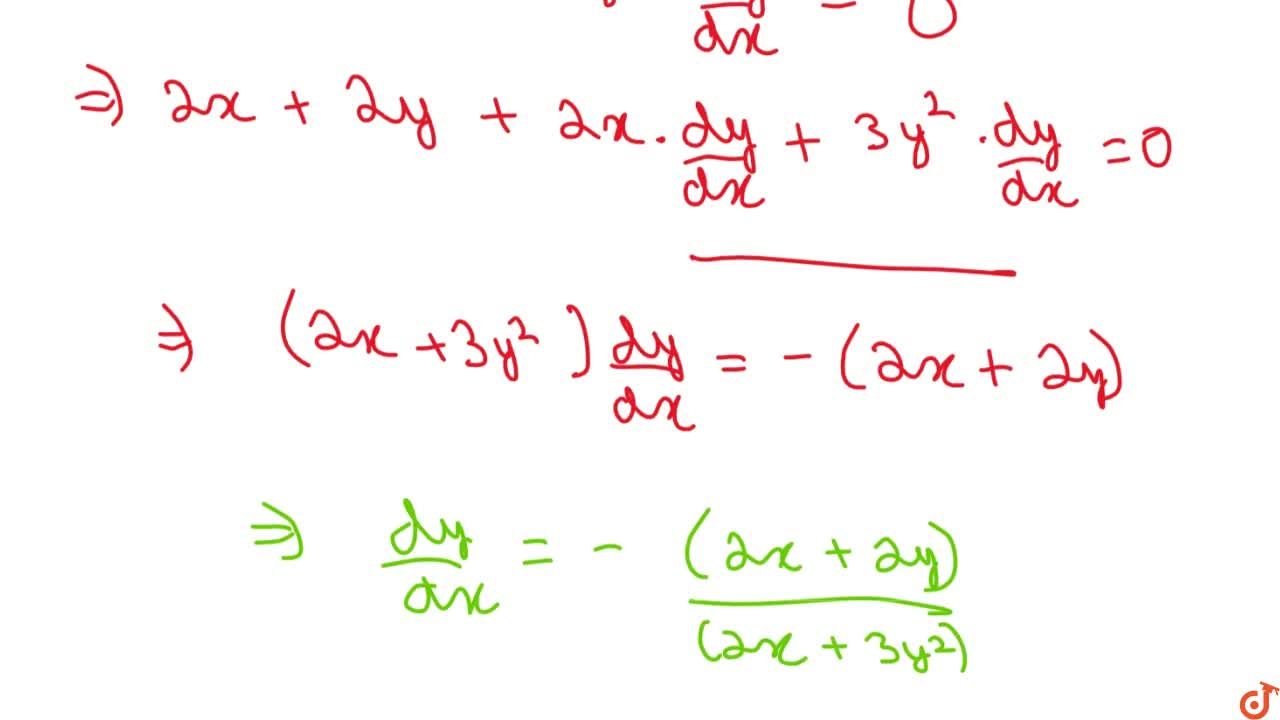 Secure Media Collegeboard Org |
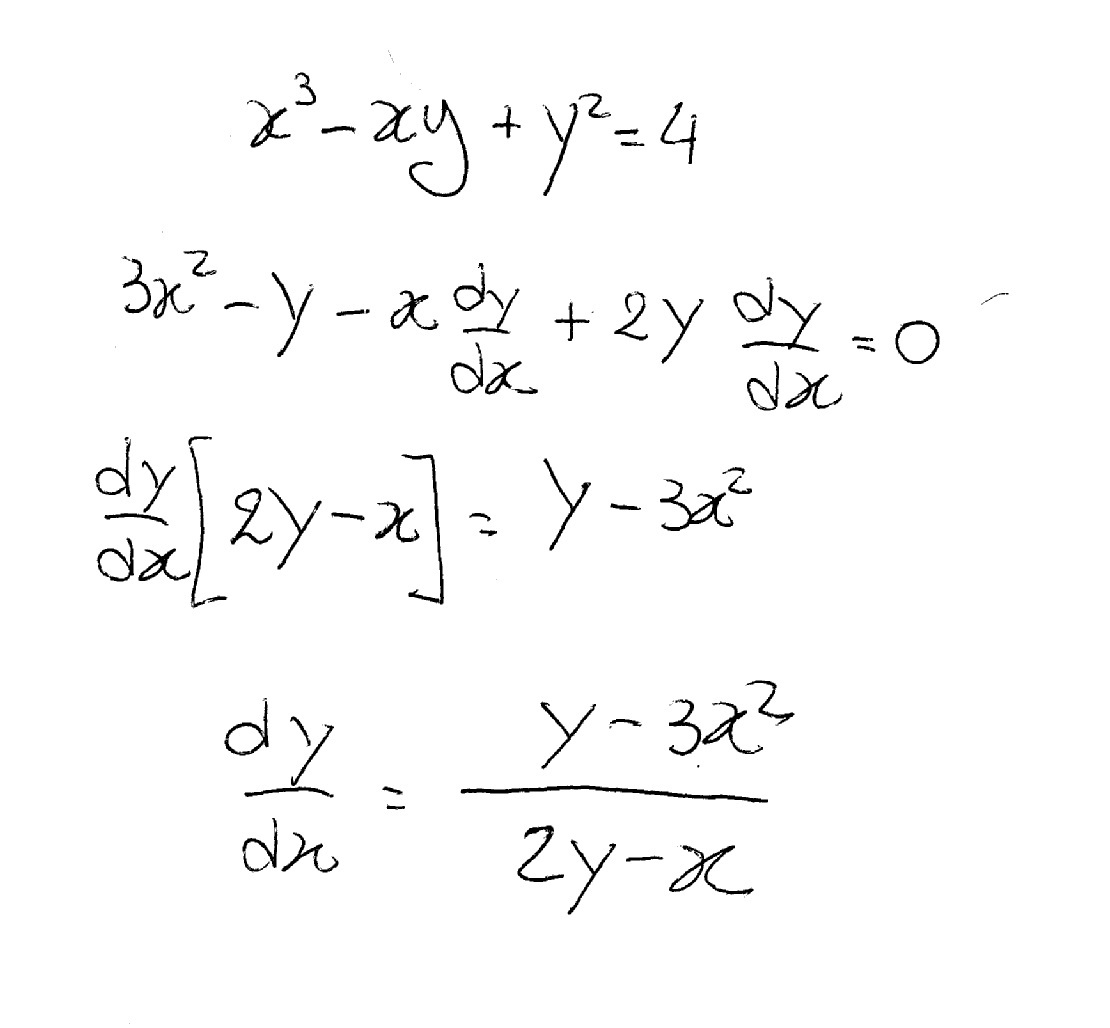 Secure Media Collegeboard Org | Secure Media Collegeboard Org |  Secure Media Collegeboard Org |
 Secure Media Collegeboard Org | Secure Media Collegeboard Org | 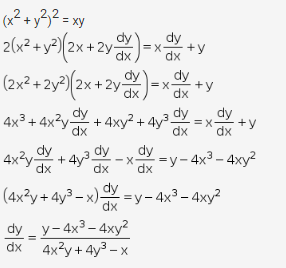 Secure Media Collegeboard Org |
 Secure Media Collegeboard Org |  Secure Media Collegeboard Org | 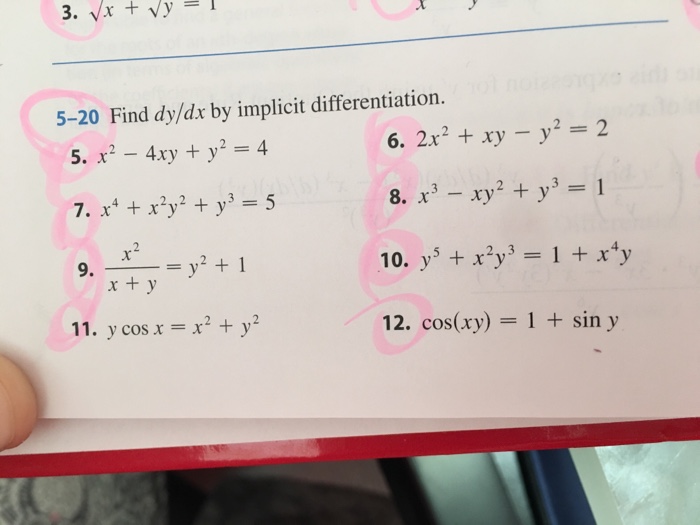 Secure Media Collegeboard Org |
 Secure Media Collegeboard Org |  Secure Media Collegeboard Org | 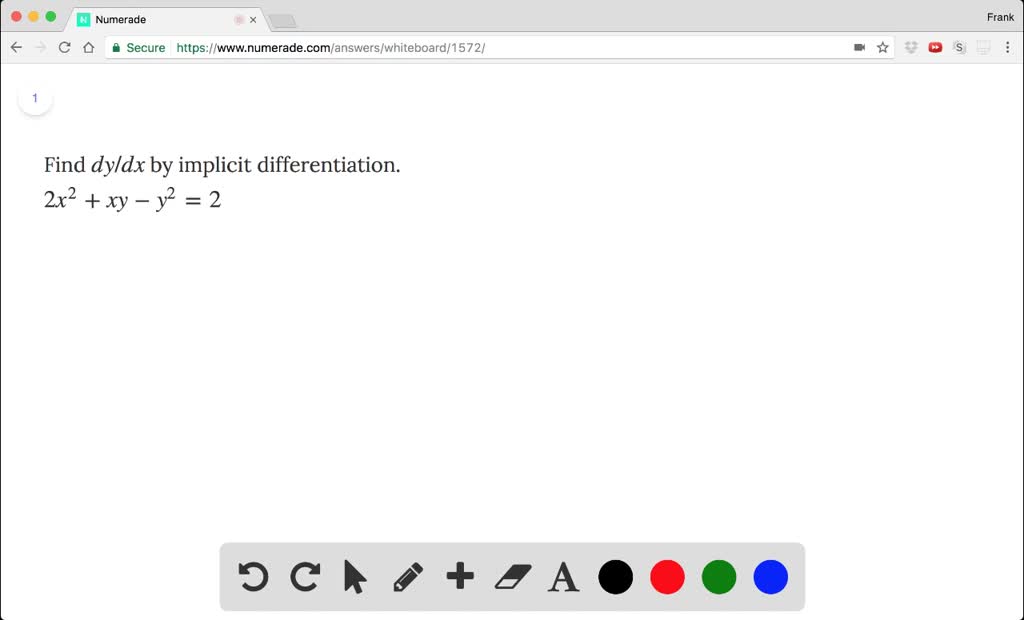 Secure Media Collegeboard Org |
 Secure Media Collegeboard Org |  Secure Media Collegeboard Org | 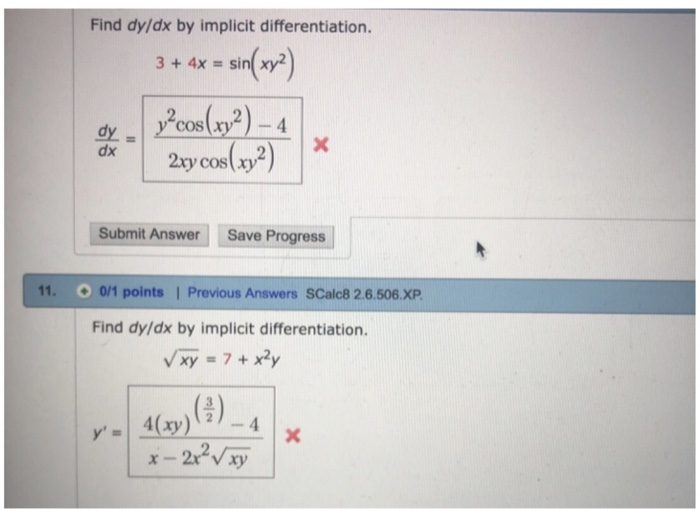 Secure Media Collegeboard Org |
Secure Media Collegeboard Org | 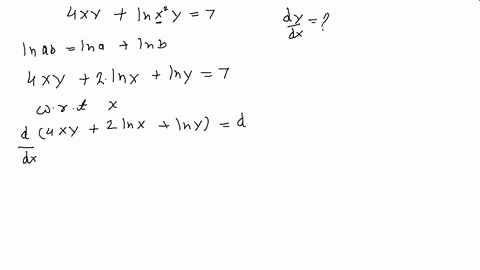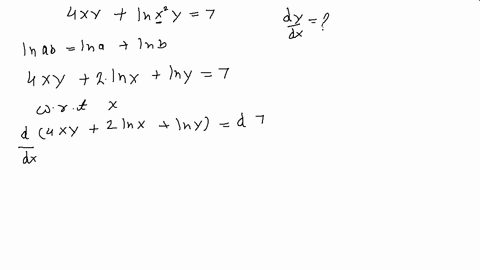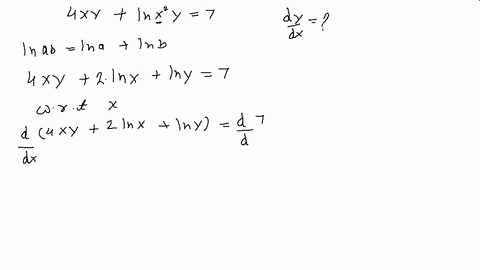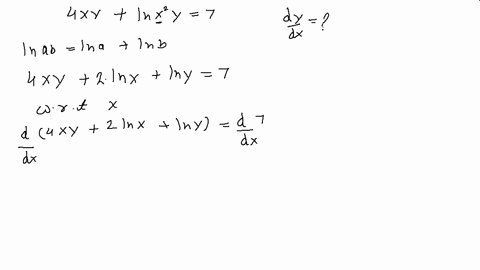 Secure Media Collegeboard Org |  Secure Media Collegeboard Org |
 Secure Media Collegeboard Org |  Secure Media Collegeboard Org |  Secure Media Collegeboard Org |
 Secure Media Collegeboard Org |  Secure Media Collegeboard Org |  Secure Media Collegeboard Org |
 Secure Media Collegeboard Org | 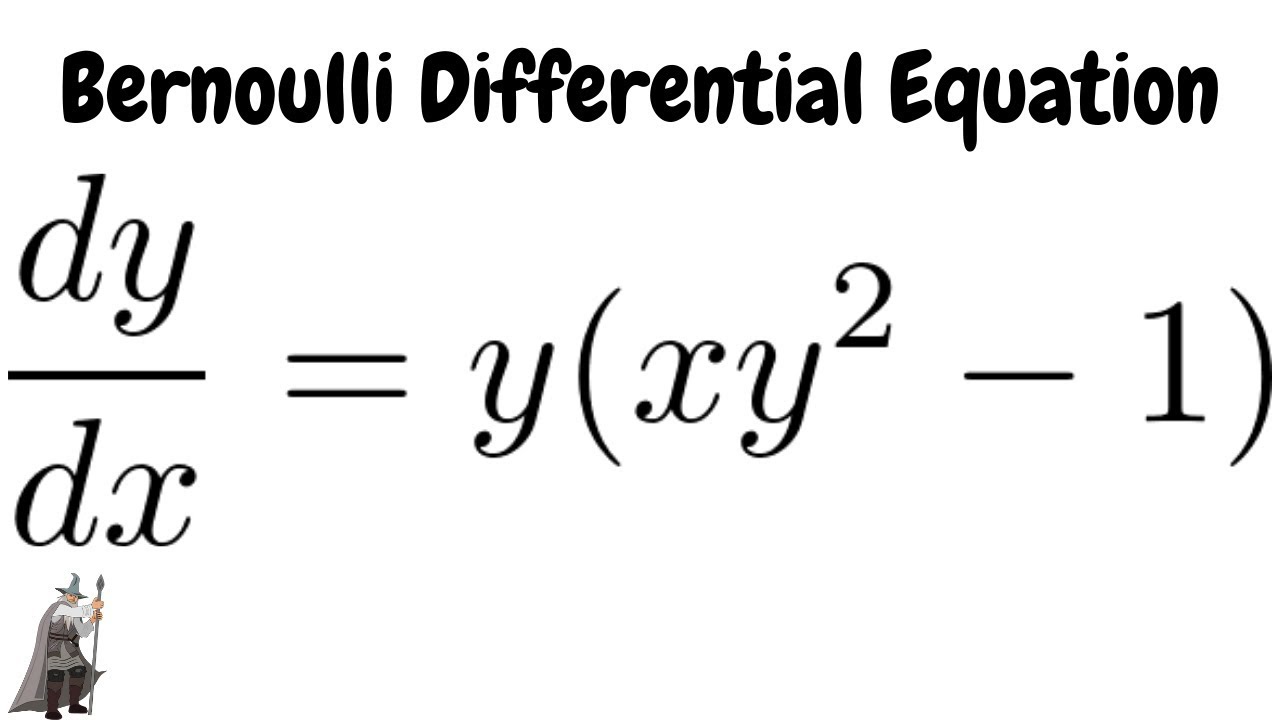 Secure Media Collegeboard Org | 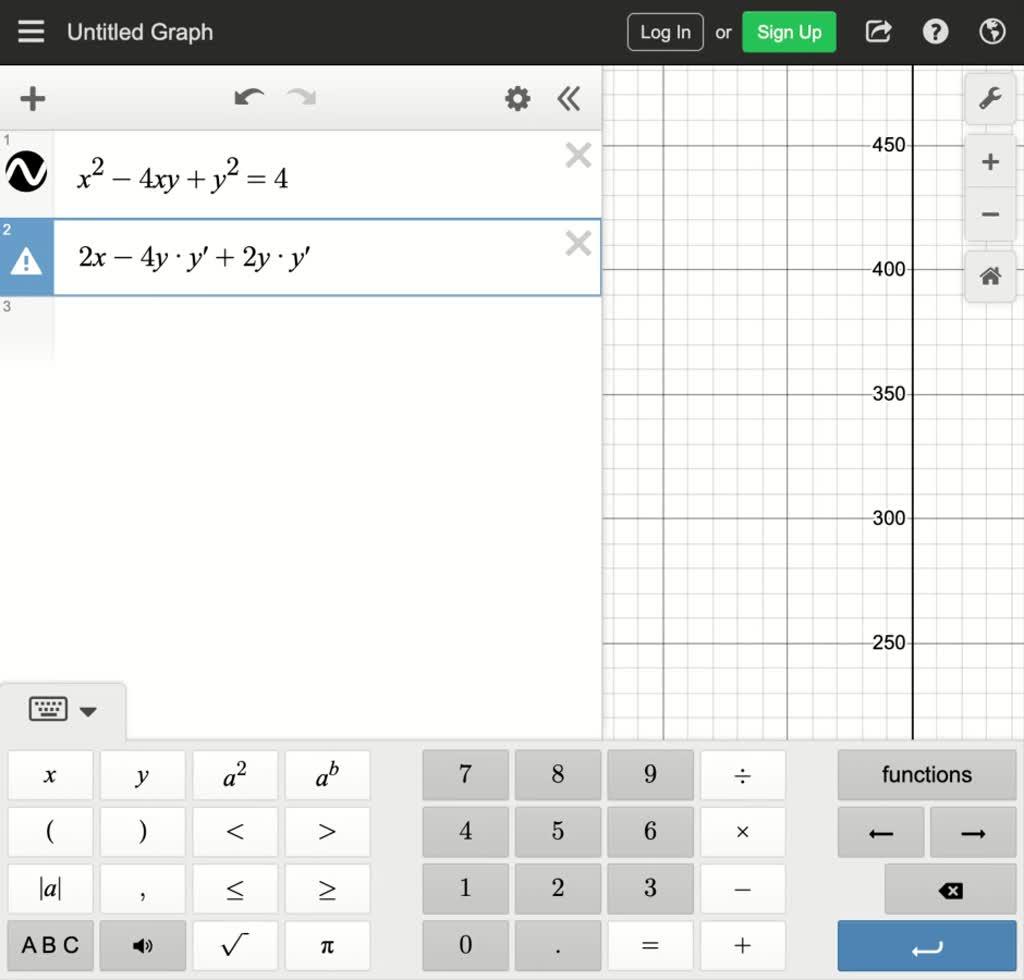 Secure Media Collegeboard Org |
Secure Media Collegeboard Org |  Secure Media Collegeboard Org |  Secure Media Collegeboard Org |
Secure Media Collegeboard Org |  Secure Media Collegeboard Org |  Secure Media Collegeboard Org |
 Secure Media Collegeboard Org | Secure Media Collegeboard Org |  Secure Media Collegeboard Org |
Secure Media Collegeboard Org |  Secure Media Collegeboard Org | Secure Media Collegeboard Org |
Secure Media Collegeboard Org | Secure Media Collegeboard Org |  Secure Media Collegeboard Org |
 Secure Media Collegeboard Org |  Secure Media Collegeboard Org |  Secure Media Collegeboard Org |
 Secure Media Collegeboard Org |  Secure Media Collegeboard Org |  Secure Media Collegeboard Org |
Secure Media Collegeboard Org | Secure Media Collegeboard Org | Secure Media Collegeboard Org |
 Secure Media Collegeboard Org |  Secure Media Collegeboard Org |  Secure Media Collegeboard Org |
Secure Media Collegeboard Org |  Secure Media Collegeboard Org | Secure Media Collegeboard Org |
Secure Media Collegeboard Org |  Secure Media Collegeboard Org |  Secure Media Collegeboard Org |
 Secure Media Collegeboard Org |  Secure Media Collegeboard Org |  Secure Media Collegeboard Org |
Secure Media Collegeboard Org | Secure Media Collegeboard Org | 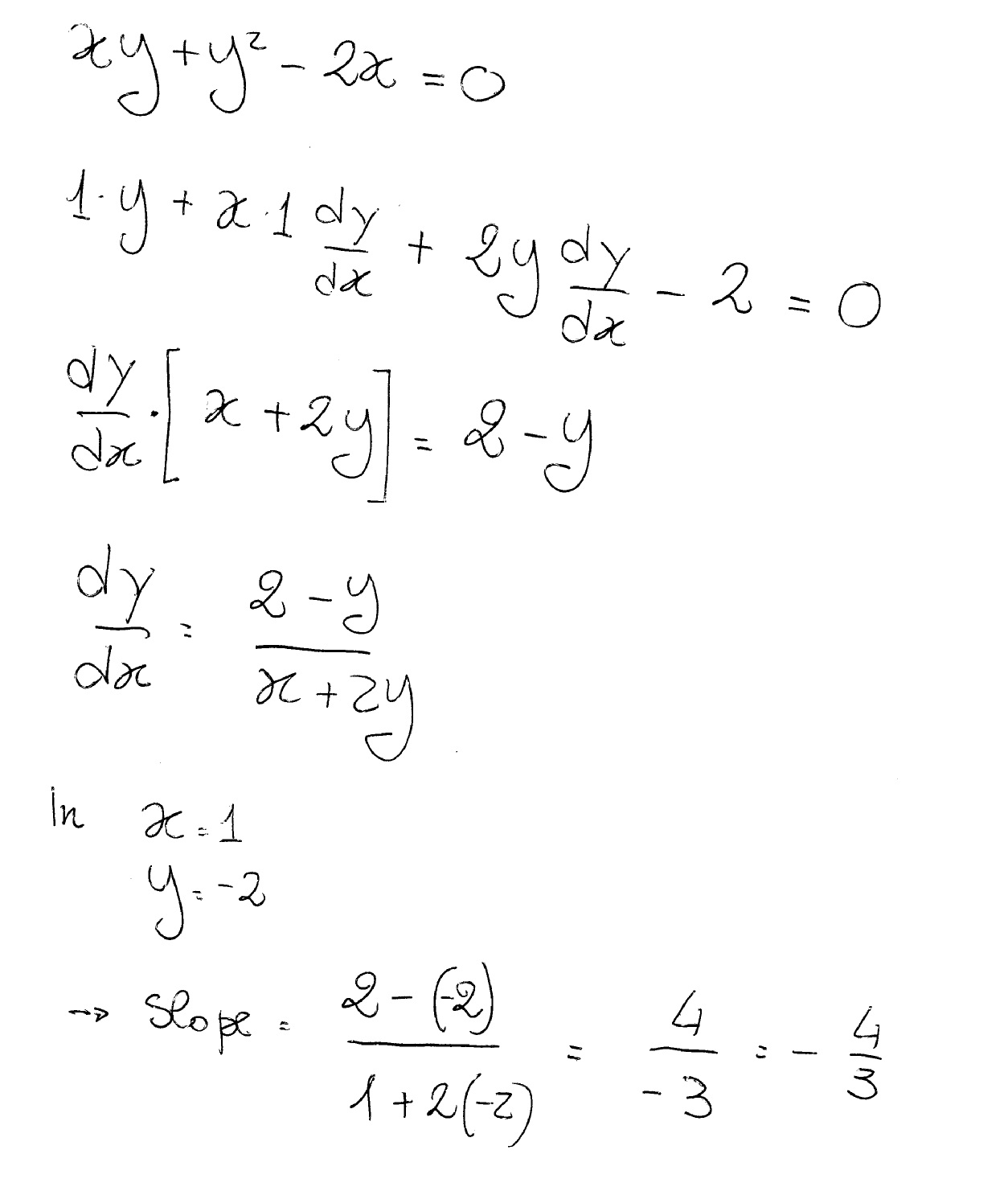 Secure Media Collegeboard Org |
Secure Media Collegeboard Org |  Secure Media Collegeboard Org | Secure Media Collegeboard Org |
 Secure Media Collegeboard Org |  Secure Media Collegeboard Org | Secure Media Collegeboard Org |
 Secure Media Collegeboard Org |  Secure Media Collegeboard Org | 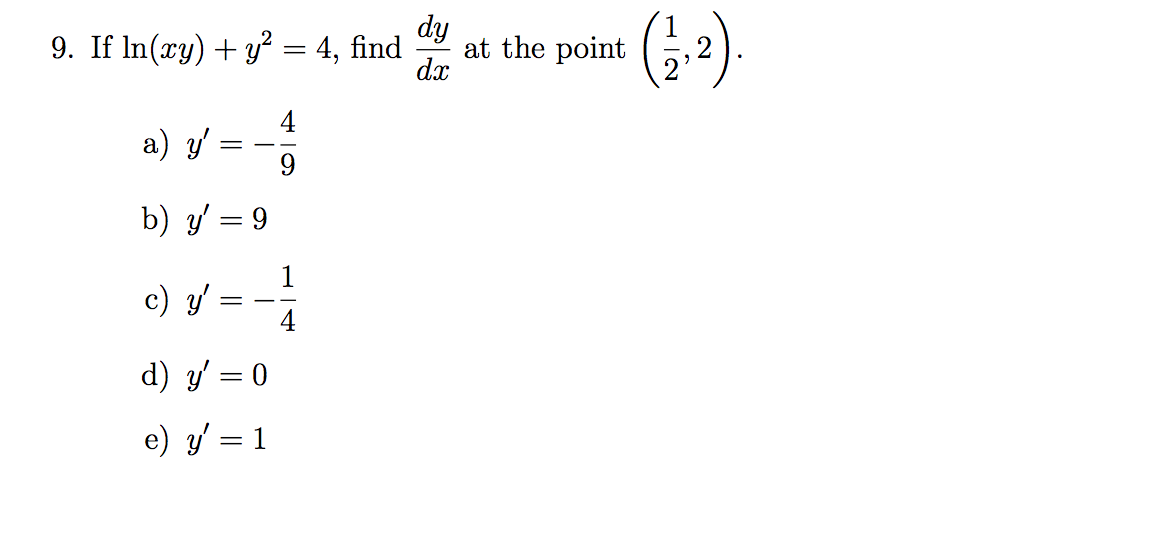 Secure Media Collegeboard Org |
Secure Media Collegeboard Org | Secure Media Collegeboard Org | Secure Media Collegeboard Org |
Secure Media Collegeboard Org |  Secure Media Collegeboard Org | Secure Media Collegeboard Org |
 Secure Media Collegeboard Org | 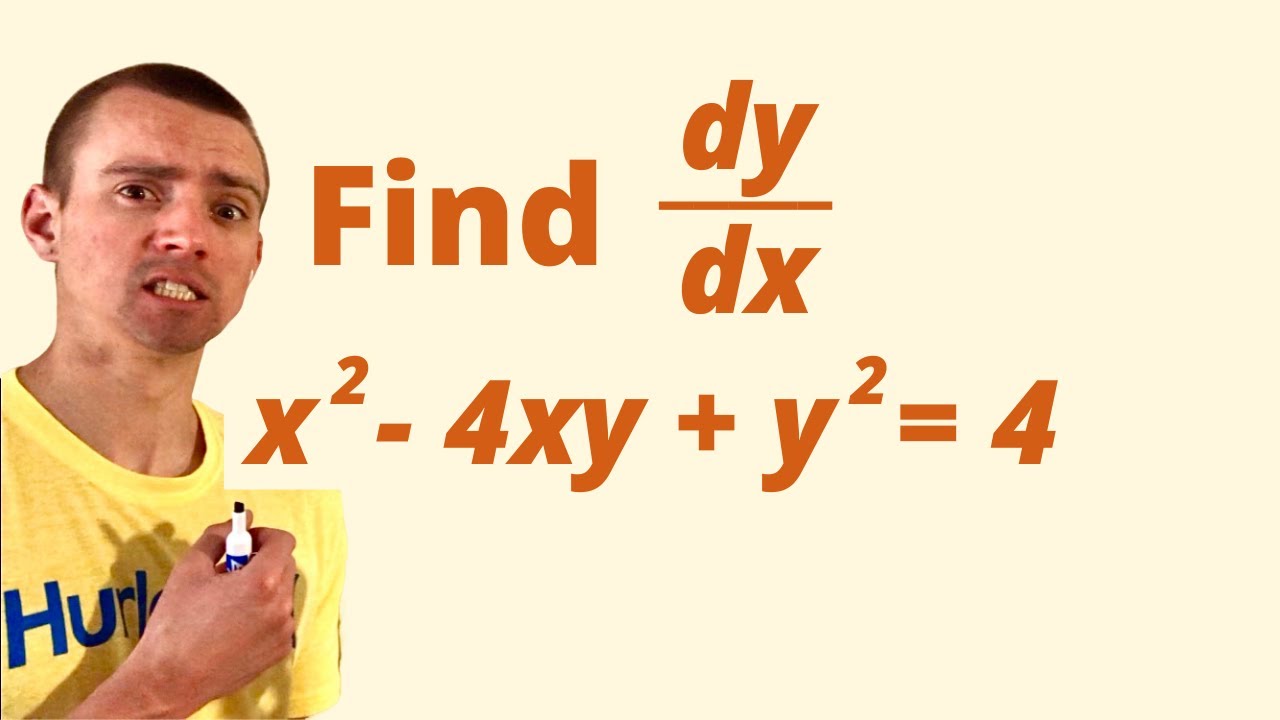 Secure Media Collegeboard Org |
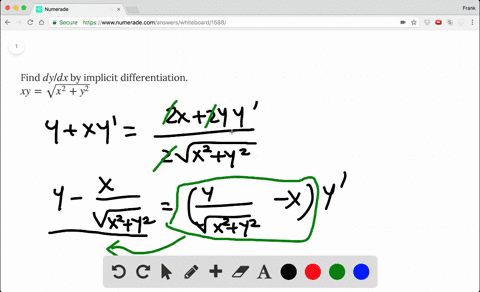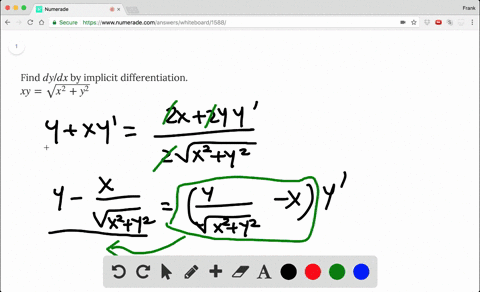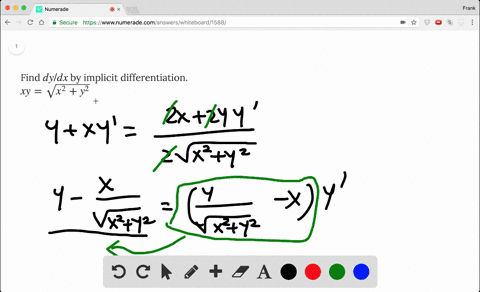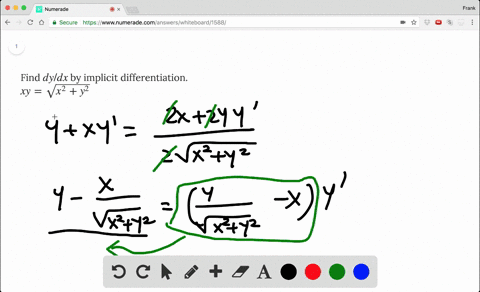
We must find dy/dx at x = 1 Assume y is a function of x, y = y(x) The relation now is xy(x) x = 1 Hence, and by the extended power rule, Substituting these results into Formula (2), we obtain We solve this equation for dy/dx Be careful!Dy dx = −x/y dy dx = −3/4 And for bonus, the equation for the tangent line is y = −3/4 x 25/4 Another Example Sometimes the implicit way works where the explicit way is hard or impossible Example 10x 4 − 18xy 2 10y 3 = 48 How do we solve for y?
Incoming Term: (x+y)^2=4 find dy/dx, x=2at^2 y=at4 find dy/dx, x^3y-2x^2+y^4=8 find dy/dx, if x=2at^(2) y=at^(4) find (dy)/(dx), 3.if x=2at2) y=at4). find (dy)/(dx), find dy/dx if (x+y)^2=4, y=log tan (π/4+x/2) find dy/dx, y=(1+x)(1+x^2)(1+x^4) find dy/dx, given that y=6x-4/x^2 find dy/dx, find (dy)/(dx) f-1.2quad (x+y)^(2)=4,




0 件のコメント:
コメントを投稿